Tretji koren na pamet

Včeraj smo si ogledali, kako na pamet hitro izračunati kvadratni koren popolnega kvadrata in ugotovili, da je zadevo za malo vaje mogoče kar hitro  izvesti. Kaj pa tretji koren popolnega kuba? Mislili bi si, da mora biti to težje. A pravzaprav ni. Tako kot je pri kvadratnem korenu potrebno vedeti kvadrate do števila 10, je pri tretjem korenu potrebno poznati tretje potence oziroma kube teh števil, potem pa gre zelo preprosto.

In zakaj naj bi bil tretji koren preprostejši od kvadratnega? Zato, ker se zadnje števke tretjih potenc števil od 1 do 10 ne ponavljajo tako kot pri kvadratih ampak so vedno različne. Tako nam ni treba ugotavljati števila enic rezultata ampak ga kar »prepišemo«. Oglejmo si dva primera, kjer bomo računali tretji koren števil 12.167 in 704.969.

Najprej izračunajmo tretji koren števila 12.167. Najprej si oglejmo zadnjo števko, torej 7. Če pogledamo naš seznam kubov vidimo, da se v rezultatu pojavlja le pri številu 3 (3³=27), kar pomeni, da bo zadnja števka rezultata seveda 3. Sedaj število, enako kot pri kvadratnem korenu, razdelimo na dva dela, le da zdaj tako, da je »ločnica« med njima pred zadnjimi tremi števkami. Dobimo 12 in 167. Zanima nas prvo, torej 12. Število v našem seznamu kubov leži med 2³ in 3³, a ker je 3³ več kot 12, kot rezultat vzamemo število 2. Rezultat je torej 23.

Kaj pa število 704.969? Postopek je enak. Pogledamo zadnjo števko in jo primerjamo s seznamom kubov. Ugotovimo, da se nahaja le pri v številu 729, ki je 9³, torej bo zadnja števka rezultata 9. Število nato razdelimo na dva dela – na 704 in 969. 704 leži med 8³ in 9³ in ker je 9³ več kot 704, upoštevamo število 8 in dobimo rezultat 89.

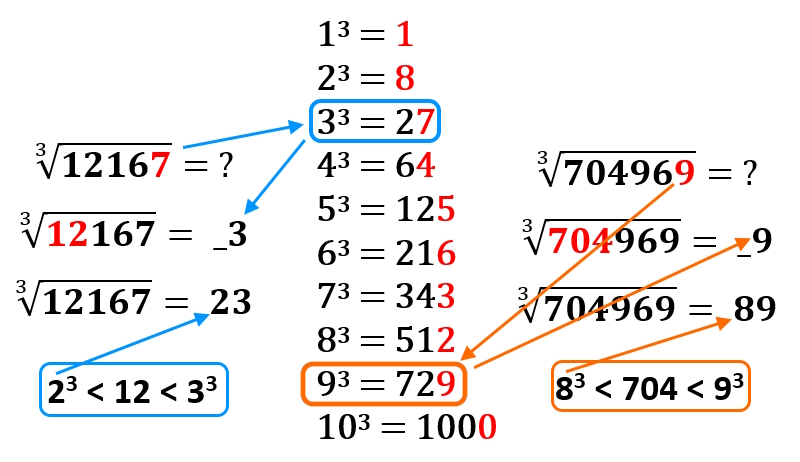
Za malce boljšo predstavo smo oboje predstavili še v obliki slike…

▪