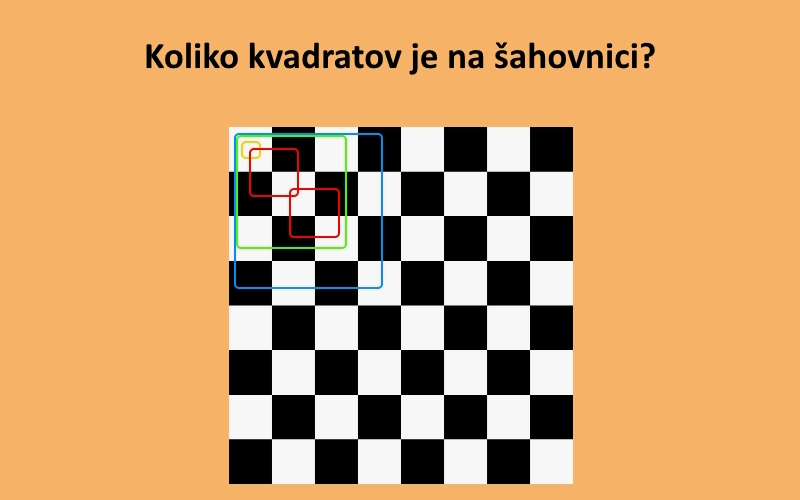
Problema se seveda lahko lotimo s preprostim štetjem, kar nas bo skoraj zagotovo pripeljalo do napačnega rezultata. Si lahko pomagamo kako drugače? Lahko. Z iskanjem vzorcev oziroma pravil. A ker je polje 8x8 kvadratkov, kot je na šahovnici, relativno veliko, se najprej lotimo manjših.
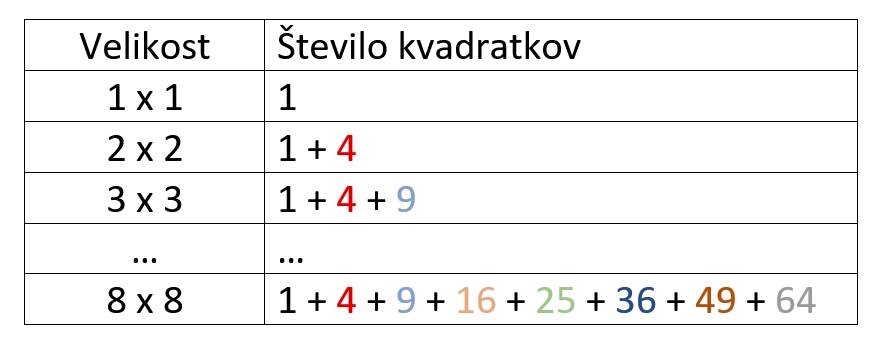
V primeru, da imamo samo eno polje, torej kvadrat 1x1, je jasno, da imamo le en kvadrat. Če imamo polje veliko 2x2, imamo 4 majhne kvadratke in enega velikega, ki ga sestavljajo vsi štirje skupaj. Pri polju 3x3 imamo devet majhni kadratkov, štiri kvadrate velikosti 2x2 in enega velikega 3x3. Zdaj se pa že nakazuje vzorec. Gre za vsoto kvadratov zaporednih števil – 1 + 4 + 9 +… Rešitev naše uganke bomo torej našli tako, da bomo sešteli prvih osem kvadratov, torej 1 + 4 + 9 + 16 + 25 + 36 + 49 + 64 in dobmo 204.
Metoda sicer deluje, a je končno seštevanje kljub temu malce zoprno. Tisti, ki se matematike malce bolj spomnite, se boste mogoče spomnili formule za izračun vsote kvadratov n zaporednih števil. Najverjetneje ste jo srečali v eno od dveh oblik:
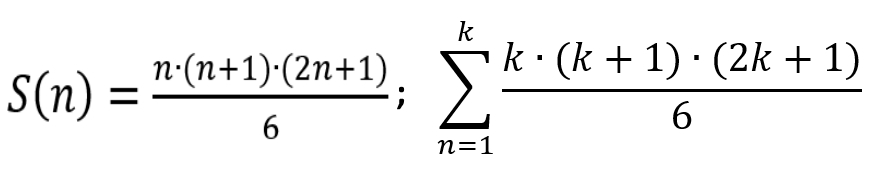
Če v to enačbo vstavite za n=8 oziroma k=8, kot se glasi naš problem, dobite rezultat precej hitreje kot če bi ročno ali na pamet seštevali. In formula je uporabna za poljubno velike »šahovnice«…▪