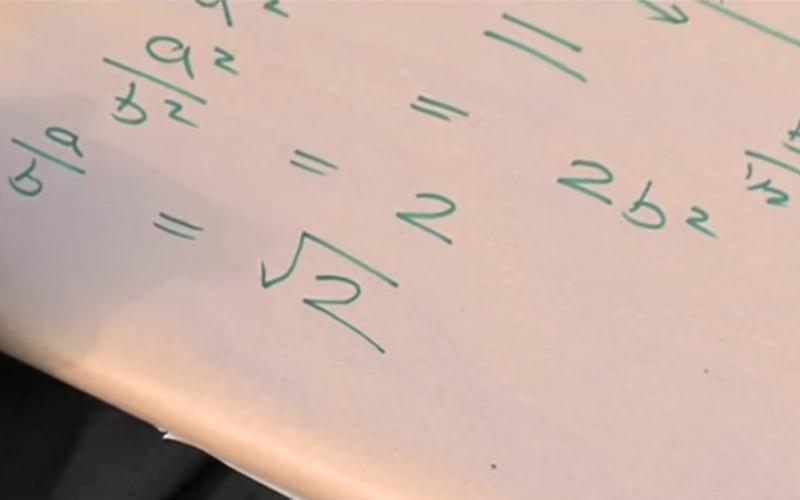A to je šele začetek. √2 ima vrednost 1,41421356…, ki nima konca, je ni mogoče zapisati v obliki ulomka a/b, kjer sta a in b celi števili. To pomeni, da gre za iracionalno število. To pa so števila, ki so jih na smrt sovražili stari Pitagorejci, ki niso bili le filozofi in matematiki ampak tudi verska sekta. Pitagorejci so menili, da je vse naravne pojave mogoče opisati s celimi števili ali razmerji med njimi. Eden od Pitagorejcev je bil tudi Hipas, ki pa je nekega dne odkril, da obstajajo tudi števila, ki jih ni mogoče predstaviti z razmerjem dveh celih števil. In takšno število lahko dobimo kar z najbolj preprostim Pitagorovim izrekom, torej nečim, kar je odkril njihov »ustanovitelj« Pitagora - če imamo pravokotni trikotnik s krajšima stranicama (katetama) dolgima eno enoto, bo najdaljša stranica (hipotenuza) tega trikotnika dolga √2. Hipas je nato matematično dokazal, da število nima konca in ga torej ni mogoče zapisati kot razmerje dveh celih števil. Odkril je nekaj, čemur sedaj pravimo iracionalna števila, kar pa mu ni koristilo ampak zelo škodovalo. Ostali Pitagorejci so bili tako jezni, da so ga odpeljali na samoten otok in ga tam pustili umreti, informacijo o odkritju pa so skrbno skrivali. Hipas je bil torej eden prvih znanstvenikov, ki je zato, ker je dokazal, da ustaljene ideje ne veljajo, izgubil življenje.
Več v videu sedaj tudi nam že zelo priljubljenega kanala Numberphile.
Vir: Numberphile/YouTube