Vzemimo, da hočemo izračunati, koliko je 102 x 231. Po običajnem postopku bi to naredili tako, da bi 102 najprej množili z 200 (z 2 in dodali dve ničli), nato s 3 (s 3 in dodali eno ničlo) in nato še z 1, vse tri rezultate pa potem sešteli. Gre pa tudi preprosteje.
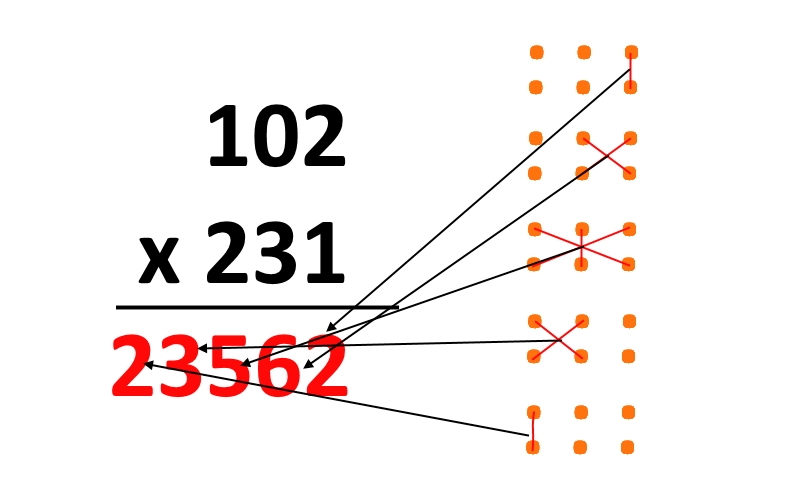
Enačba vsebuje dve trištevilčni števili, zato si kot pomoč na desni narišimo petkrat po dve vrstici s po tremi pikami. Zakaj? Bo kar hitro jasno. Vsaka od petih vrst namreč pomeni kombinacijo števil, ki jih moramo zmnožiti, da dobimo končni rezultat. Kot vidite, sta v prvi vrsti povezani skrajno desni piki kar pomeni, da moramo zmnožiti skrajno desni števili, v našem primeru je to 2 x 1= 2. V drugem koraku imamo narisan križec, ki povezuje zadnjo piko prve vrstice in drugo piko druge ter obratno. To pomeni, da moramo množiti število enic prvega števila s številom desetic drugega, nato pa temu prišteti produkt števila desetic prvega in števila enic drugega, torej 0 x 1+ 2 x 3 = 6. A vidite vzorec? Seveda ga… V tretjem koraku bo vsota 1 x 1 + 0 x 3 + 2 x 2 = 5, v četrtem 0 x 2 + 3 x 1 = 3, v petem pa 1 x 2 = 2 . In rezultat? Ta je seveda 23562 oziroma rešitev posameznih korakov. Dokaj preprosto in hitro. Seveda so narisane pike le kot pripomoček, ki ga z nekaj vaje lahko opustimo in rezultat dobesedno kar pišemo.
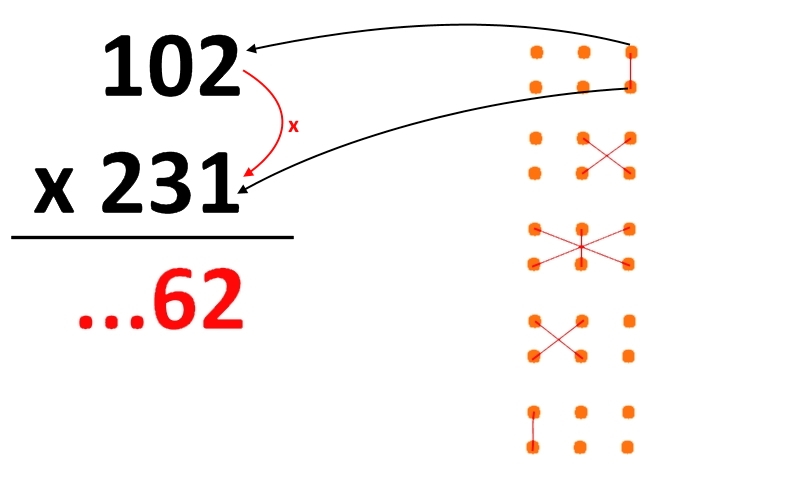
Kaj pa, če je eno število dvo-, drugo pa triševilčno? Ni težav, saj moramo pred dvoštevilčnega zapisati le ničlo in nadaljevati po enaki metodi. Seveda pa je potrebno paziti, da v primeru, ko je vsota več kot 9, naslednje število v rezultatu ustrezno povečamo.
▪