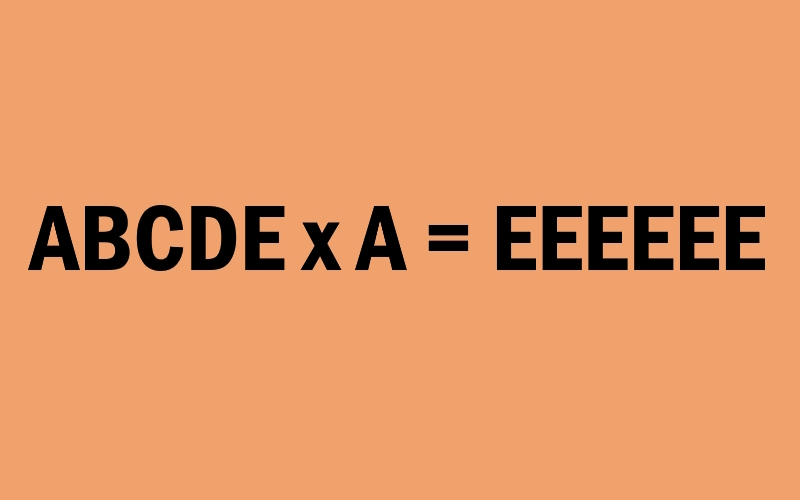In kako se glasi naloga? Imamo neko petmestno število ABCDE, ki ga pomnožimo z A in dobimo šestmestno število EEEEEE. V nalogi vsaka črka ponazarja drugačno števko, ABCDE pa ne pomeni, da si števke sledijo po velikosti ali da je med njima razlika 1 (lahko pa je). Najdite števila A, B, C, D, in E.
Bi jo znali rešiti vi? Poskusite. Če ne bo šlo, je spodaj rešitev.
Rešitev
Zadeve se je potrebno lotiti po sistemu izločanja.
Najprej razmislimo ali je mogoče, da je A=1. Kaj hitro vidimo, da ne, saj bi ABCDE zaradi množenja z A=1 moral biti enako EEEEEE, kar seveda ni mogoče. Torej ne more biti 1.
V naslednjem koraku se osredotočimo na enice. Vidimo, da mora veljati, da mora biti rezultat E x A enak številu, ki ima E enic. Katera števila so takšna? Če malce razmislimo oziroma si ogledamo tablico množenja vidimo, da je takšnih možnosti 8:
Štiri so večkratniki števila 6: 2 x 6 = 12, 4 x 6 = 24, 6 x 6 = 36, 6 x 8 = 48 in
Štiri so večkratniki števila 5: 5 x 3 = 15, 5 x 5 = 25, 5 x 7 = 35, 5 x 9 = 45.
Ker E in A ne smeta biti enaka, odpadeta možnosti 6 x 6 in 5 x 5, torej jih ostane le še šest. Zapišimo jih kot pare, da bomo imeli boljši pregled:
(A,E) = (6,2), (6,4), (6,8) in
(A,E) = (3,5), (7,5), (9,5).
Pa preizkusimo eno in drugo. Zadeve se najlažje lotimo tako, da enačbo pretvorimo iz množenja v deljenje. Ker mora veljati, da je ABCDE x A = EEEEEE, mora seveda veljati, da je EEEEEE : A = ABCDE. Če zdaj namesto E in A vstavljamo števila iz zgornjih parov dobimo
222222 : 6 = 37037
444444 : 6 = 74074 in
888888 : 6 = 148148.
Ker noben rezultat ne daje števila, ki bi imela same različne števke, poskusimo z E = 5:
555555 : 3 = 185185
555555 : 7 = 79365
55555 : 9 = 61728,33.
Vidimo, da prva in zadnja možnost odpadeta, druga pa je rešitev. Račun se torej glasi 79365 x 7 = 555555.
Simpatičen izziv, a vsekakor mnogo prezahteven za povprečnega devetletnika, ne glede na to, od kod je...
▪